Closed An introduction to algorithm complexity and big o/theta/omega notation [eclipse]

[Strawberrry]

Introduction to Algorithm Complexity and Big-O notation

Introduction:
It is common for coders to jump straight into writing code, without thinking about the best way to do things. There have been many alternative algorithms written for common things, such as sorting lists, and some are much better than others. This tutorial is designed to introduce you to algorithm complexity analysis, and the big O (pronounced "big oh") notation. This will help you understand more about the best way to write algorithms to minimize time and memory usage.



What is algorithm complexity, and why should I care about it:

Algorithm complexity is just a way to formally measure how fast a program or algorithm runs. We cannot just write the code and time how fast it runs in practise, because many things affect the runtime in practise (such as the processor you are using, RAM, bus speeds, etc). So algorithm complexity analysis is designed to compare algorithms in theory, to see which is the most efficient.

It is important to be aware, at least partially, of different algorithm complexities so you don't end up accidentally writing algorithms that take 10 times longer than necessary. Even if you don't need to be able to recognize instantly whether an algorithm is linear time or exponential time, this tutorial should give you an idea about which is which, because such things will become very important when you are dealing with massive amounts of data or large numbers.



Terminology:

Fundamental Instruction - the simplest operations, for example assigning values to variables, comparisons, retrieving values from arrays, basic arithmetic (addition, multiplication, incrementation, etc). Don't worry, we aren't just going to count these.
Worst case analysis - pretty self explanatory, this just means that if we have an algorithm, we analyse it by assuming we are as unlucky as possible with the input (i.e. the input that will cause the algorithm to do the most work)



Asymptotic Behaviour:

An asymptote is something which occurs when a function gets closer and closer to a value as its input changes, but never quite reaches it. We can use this by only keeping the largest growing part of the function, because that will have the most influence on the output as it gets large. We also ignore any coefficients. For example, 3n + 2 becomes just n, and 2n^3 + 4n + 2 just becomes n^3. This is a little bit of maths involved, because you need to understand what functions grow faster than others. Example: 1 < sqrt < n < n^2 < n^3 < etc.

This site provides a great reference sheet for comparing the complexities of different common algorithm implementations: You do not have permission to view the full content of this post. Log in or register now.




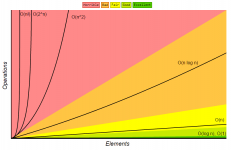
Complexity in code:

Now that we understand what asymptotic behaviour of functions is, we can start looking at some code to find the complexity of the algorithms in practise. The biggest thing we look for in code is Loops, because loops are the things which will cause the fundamental instructions to be repeated over and over rather than a constant amount.

A function without any loops is constant, i.e. f = 1.
Example:

int x = 1;
int y = x + 2;
if(x == 1) {
   System.out.println(x);
1}

A function with a single loop that loops n times is f = n, because it will repeat the instructions in the loop n times. We ignore how many fundamental instructions are in the loop, because of the asymptotic analysis, because more instructions is just a coefficient of n (e.g. 4n) which is then ignored.
Example:

int n = 10;
for(int i = 0; i < n; i++) {
   System.out.println(i + x);
}

in this loop, each time the loop occurs it executes multiple fundamental instructions e.g. comparison i < 2, incrementation i++, addition i + x, etc. but these are constant each time, so it is ignored - the number of times the loop occurs is the biggest influence.

A function with nested loops, e.g. a loop inside a loop, is just a power of n.
Example:

int n = 10;
for(int i = 0; i < n; i++) {
   for(int j = 0; j < n; j++) {
       System.out.println(i + j);
   }
}

This function has f = n^2 because the inside loop loops n times for each outside loop, giving n * n = n^2
By the same logic, a loop inside a loop inside a loop is f = n^3.



Big Ɵ (Big Theta) Notation

Up until now we have been using f = something to represent the complexity. Actually, we use Ɵ (theta) instead of f, like this:
if f = n^3 then we write Ɵ(n^3)
This is known as Big-Ɵ notation. (The character Ɵ is the greek letter theta.)
This notation is used when we know exactly the complexity of a function. But sometimes we may not know exactly what complexity it has, only a maximum / minimum complexity. So we then introduce 2 new notations - Big O and Big Omega notations to provide a maximum and minimum complexity.



Big O Notation

Big O notation is like a maximum complexity we know that a function has. All we know, when we use this notation, is that the true complexity (Big Ɵ) is the same of less than the Big O complexity. Technically, we say that O(f) is a 'set' of functions that have the same of larger complexity, so Ɵ(f) is always in O(f) but not the other way around. For example, we can say that the function f = n is part of O but also O(n^2), O(n^3) or anything bigger. But we try to find the lowest possible because that is the most helpful obviously.

Usually we can never actually know if we have found the most efficient algorithm for a particular task, for example the most efficient algorithm to sort a list into order, so we use the Big O notation on existing algorithms to show that the most efficient solution is either the same or better than the existing ones.

Example of a sorting algorithm in Java, this is an implementation called the BubbleSort:

int currentMinIndex = 0;

for (int front = 0; front < intArray.length; front++)
{
    currentMinIndex = front;

    for (int i = front; i < intArray.length; i++)
    {
        if (intArray[i] < intArray[currentMinIndex])
        {
            currentMinIndex = i;
        }
    }

    int tmp = intArray[front];
    intArray[front] = intArray[currentMinIndex];
    intArray[currentMinIndex] = tmp;
}

We can see that this implementation has a loop inside a loop. As we saw, if we have a loop that iterates n times inside a loop which iterates n times, then we have f = n. So the Big O notation for this algorithm is O(n^2) (in the worst case analysis. Best case - an already sorted list - gives O). But this is not the most efficient sorting algorithm and in fact other algorithms have been created which have O(n * log n) which is better. That is why we use Big O notation, because this is an upper bound of the sorting algorithm. In general, Big O is easier to work out that Big Ɵ because we can actually make the algorithm worse efficiency to make it easier to work out, and end up with the upper bound even if its not the best possible.



Other Notations

There are actually 5 unique sets of functions that you might see. These are:
o(f) - Little o - same as Big O but it is never equal to, always less than. We say that Ɵ is a Proper subset of o
O(f) - Bit O - As we have already seen. Can be equal to or less than. We say Ɵ is a subset of O
Ɵ(f) - Big Theta - pretty much just 'equal to'. This is also the interection of O(f) and Ω(f).
Ω(f) - Big Omega - The opposite of Big O, this acts as a lower bound. Ɵ(f) will always be equal to or worse than Omega(f). Technically, Ɵ is a superset of ω
ω(f) - Little Omega - to Big Omega what Little o is to Big O. Ɵ(f) will always be worse than Omega(f). Technically, Ɵ is a Proper superset of ω



Special thanks to MeshCollider

 

[Arcturus]

First blood, Salamat sa time ts. Malaking tulong to sa mga tulad ko

 

[Strawberrry]

First blood, Salamat sa time ts. Malaking tulong to sa mga tulad ko

Hahahaha salamat pre, 10 secs lang hinihingi ko sa inyo para mag pa salamat hahahah salamat

 

[dragit22]

salamat sakto topic namin sa mathematical computing. May pdf po ba kayo about algorithm complexity at saka data manipulation?